• Ein leeres Wort ist ein Palindrom.
• Ein Wort aus einem Buchstaben ist auch ein Palindrom.

• len(a) gibt die Länge des Strings wieder
• list(a) wandelt den String in eine Liste von Buchstaben um
• a[0] ist "H"
• a[-1] ist "o"
• a[4] ist "o"

Implementiere rekursiv eine Treppe mit 6 Stufen. Denke hier an eine geeignete Abbruchbedingung und löse dies nicht iterativ!

1. Implementieren Sie eine Funktion, die folgende Zeichnung mit variablen Eingabeparametern zeichnet. Die zugrundeliegende Figur besteht aus 4 gleichlangen Abschnitten, alle auftretenden Winkel sind 60 oder 120 Grad.

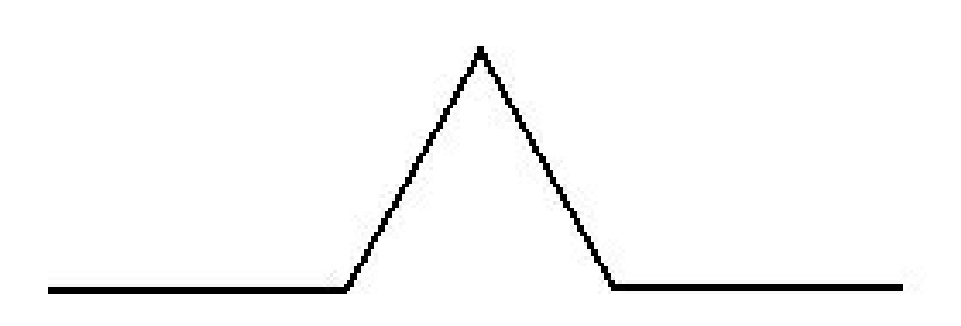
2. Wenn man nun statt der hier gezeigten Strecken wieder dieselbe Figur (verkleinert!) verwendet, dann erhält man das folgende Bild. Implementieren Sie unter Zuhilfenahme der in 1) erstellten Funktion, diese Darstellung.

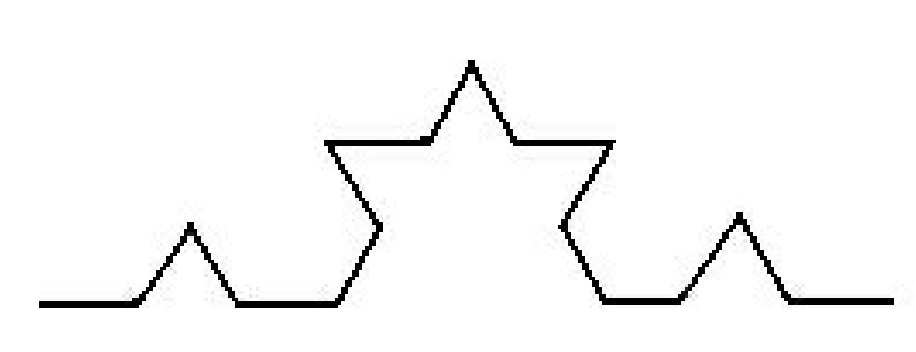
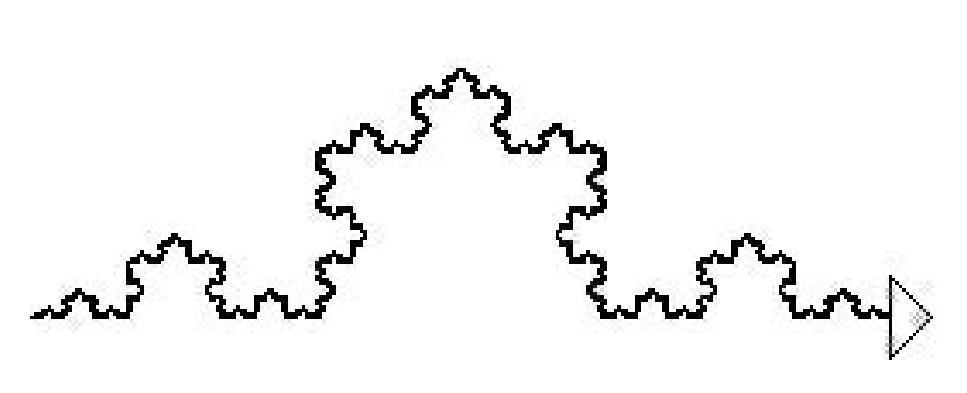
3. Und wenn man das nun ein paar mal "ineinander" schachtelt, dann ergibt sich die "Koch'sche Kurve". Der Trick ist also: solange die zu zeichnende Strecke noch länger als eine bestimmte Grenze ist, ruft die Zeichenprozedur sich selbst vier mal auf; wenn die Streckenlänge die Grenze unterschritten hat, wird stattdessen der obige Streckenzug aus den 4 Strecken gezeichnet. Schreiben Sie ein Programm, das die Koch'sche Kurve zeichnet.


4. Wenn Sie die Koch'sche Kurve 6 mal auf die Seiten eines regelmäßigen Sechsecks zeichnen, erhalten Sie die Koch'sche Schneeflocke, die tatsächlich eine gewisse Ähnlichkeit mit einer echten Schneeflocke hat. In der Natur sind rekursive Strukturen sogar relativ häufig anzutreffen, wenngleich die Rekursionstiefe dabei meist recht klein ist. Implementieren Sie die Koch'sche Schneeflocke.

1. Geben Sie eine Rekursionsvorschrift (Funktion, Abbruchbedingung und Rekursionsschritt) für die Bestimmung der Bakterienzahl nach n Stunden an.

2. Implementieren Sie die Funktion und berechnen Sie, wie viele Bakterie nach 24 Stunden da sind.

3. Setzen Sie das Bakterienwachstum grafisch mit dem Turtle-Modul um. Dabei soll das Wachstum langsam pro Stunde angezeigt werden.

            # Hiermit können Sie eine Wartezeit festlegen
            import time

            # programm sleeps for 5 seconds and 300 miliseconds
            time.sleep(5.3)
          

                  
                def potenzVonZwei (n):
                  return 2 * potenzVonZwei (n - 1)
                  
                

1. Warum funktioniert die Funktion nicht? Was wurde vergessen? Korrigieren Sie die Fehler.
2. Mit welchem Aufruf lässt sich dann die Anzahl der Reiskörner auf dem 64. Feld des Schachbretts berechnen?
3. Schreiben Sie eine weitere Funktion, die die Gesamtsumme der Reiskörner bis zum jeweiligen Feld berechnet.
4. Schreiben Sie eine weitere Funktion, die die das Gesamtgewicht der Reiskörner auf einem beliebigen Feld berechnet. Ein Reiskorn wiegt in etwa 65 mg.
5. Schreiben Sie eine weitere Funktion, die die die Gesamtfläche berechnet, die die Reiskörner auf einem beliebeigen Feld auf dem Boden verteilt einnehmen würde. Gehen Sie von einer quadratischen Fläche aus. Ein Reiskorn hat die Volumenmaße 2 mm * 2 mm * 1cm.
6. Schreiben Sie eine weitere Funktion, die die Anzahl an Milchpackungen berechnet, die nötig sind, um Platz für die Reiskörner auf einem beliebigen Feld zu garantieren.
7. Verallgemeinern Sie die Funktion aus der vorherigen Aufgabe, indem diese ein Volumen übergeben bekommt und ausrechnet wie viele dieser Volumen gebraucht werden, um die Reismenge aufzunehmen. Teste Sie ihre Funktion mit der durchschnittlichen Ladung eines PKW, LKW, Flugzeug, Containerschiff und Fußballstadien. Nehmen Sie für die Volumenberechnung der Beispiele ungefähre Werte.