Rekursion in grafischen Lindermayer-Systemen
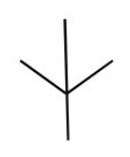
Spross mit Dreifachverzweigung
Unter Zuhilfenahme der Turtle können wir L-Systeme, die wir durch Rekursive Funktionen erzeugen sichtbar machen. In dieser Aufgabe betrachten wir einen Spross einer Pflanze. Dieser verzweigt sich nach einem gerade Stück in 3 gleich große Verzweigungen. Mit diesem Ausgangspunkt soll rekursives Wachstum abgebildet werden. Dazu sollen die Verzweigungen wieder durch das gleiche Wachstum (Spross mit Dreifachverzweigung aber nur noch mit der Hälfte der Größe) rekursiv ersetzt werden.
Die Lösung durch Rekursion entwickeln wir, wie in der Vorlesung vorgeführt, zuerst durch Realisierung des Basisfalls. Dieser zeichnet zuerst das Grundsystem. Dies geschieht innerhalb einer Funktion, da dies eine Lösung der funktionalen Programmierung ist. Versuchen Sie es direkt einmal selbst ohne in die Lösung zu schauen. Falls dies nicht schaffbar ist, dann hangelt man sich durch folgende algorithmische Beschreibung. Falls diese auch nicht helfen sollte, dann schaut man sich die Lösung an, deckt diese wieder zu und versucht Sie dann ohne die Lösung den Code zu schreiben.
- Importieren des Turtle Package
- Definition einer Funktion mit den Namen plant oder ähnlich mit Parameter laenge.
- Wir zeichnen die Figur von unten nach oben. Zuerst gehen wir also nach vorne und zwar soweit wie der Parameter laenge es vorgibt
- Dann Drehung nach links um 45 Grad.
- Dann wieder nach vorne um den Wert leange.
- Dann zurück um den Wert laenge.
- Dann nach rechts um 45 Grad.
- Dann nach vorne um den Wert laenge.
- Wieder zurück um den Wert leange.
- Dann nach rechts um 45 Grad.
- Dann nach vorne um den Wert laenge.
- Wieder zurück um den Wert leange.
- Jetzt ist es wichtig, dass wir ganz zurück zum Ausgangspunkt gehen, damit wir später in der Rekursion einzelne Komponenten komplett ersetzen können! Also links 45 Grad und dann zurück um den Wert laenge.
- Probiere das Programm nun aus indem Sie außerhalb der Funktionsdefinition
Turtle.left(90)aufrufen, damit der Baum vertikal gezeichnet wird und dann die Funktion aufrufen mit plant(150).
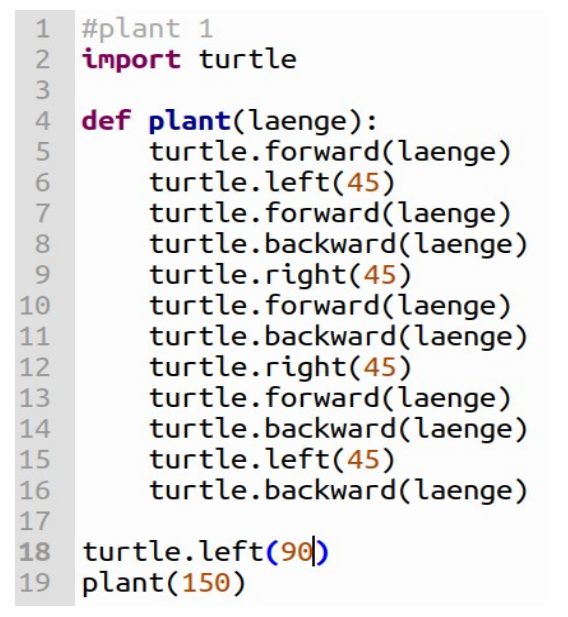
Grundsystem - L-System
Jetzt wird der Spross gezeichnet. Es fehlt eine Abbruchbedingung mit der die Rekursion beendet werden kann und wir verhindern, dass eine Endlosausführung generiert wird.
- Deshalb bekommt unsere Funktion einen zweiten Parameter tiefe. Dieser kontrolliert die Tiefe der Verschachtelung der Rekursion.
- Wenn die letzte Verschachtelungstiefe erreicht wurde, dann soll der Spross mit seinen Verzweigungen gezeichnetwerden und nicht die Rekursion weitergeführt werden. Deshalb wird das Zeichnen des Sprosses nun in eine if-Bedingung gesetzt, die war ist wenn die letzte Rekursionstiefe erreicht wurde, also
tiefe == 0ist. - Damit haben wir jetzt den Basisfall abgeschlossen und können die Funktion mit
plant(150,0)aufrufen.

Basisfall - L-System
Jetzt kommen wir zum Rekursionsfall. Hier wollen wir eine Rekursion aufbauen, indem die Zweige des Sprosses bei jedem Rekursionsaufruf ersetzt werden durch einen Spross der halben Größe. Der Rekursionsfall geschieht in der Umsetzung solcher L-Systeme immer im else-Block.
- Mache dir – auch zeichnerisch - klar, was im Rekursionfall gezeichnet werden soll. Dies ist sehr ähnlich zum Basisfall aber ergänzt bzw. verändert durch die Rekursionsaufrufe. Zuerst soll die Turtle vorwärts gehen. Diesmal aber nicht um den Wert länge, sondern nur um die Hälfte der Länge. Damit haben wir den Zweig gezeichnet und kommen nun zu den Verzweigungen.
- Im Basisfall geht nun die Turtle 45 Grad nach links. Dies können wir für den Rekursionsfall übernehmen, da hier auch jede Verzweigung mit dem Winkel gezeichnet werden soll.
- Im Basisfall geht die Turtle nun vorwärts und dann rückwärts um den Wert der Länge. Dies können Sie im Rekursionsfall nicht beibehalten, da die Verzweigungen genau die Strecken sind, die Sie ersetzten sollen. Hier wird nun stattdessen der Rekursionsaufruf stattfinden. Also an der Stelle der Verzweigung soll ein neuer Spross halber Länge entstehen. Dies können wir durch den Aufruf unserer Funktion mit neuen Parametern erreichen →
plant(laenge / 2, tiefe – 1). Wir vermindern hier die Tiefe jeweils um 1, damit wir ein Ende der Rekursion erreichen können. - Man ersetzt hier sowohl die vorwärts- wie auch die rückwärts- Anweisung. Dies liegt daran, dass im Basisfall auch schon der Rückweg vollständig implementiert ist. Dies sollte man durch zeichnen und debuggen des Codes nachvollziehen. Wenn man diesen Punkt nicht verstanden hat, kann man diese Lösung nicht auf ähnliche Probleme übertragen.
- Verfahre mit den anderen 2 Verzweigungen ebenso.
- Übrig bleiben die letzten 2 Anweisungen des Basisfalls, die man auch übernehmen kann, da die Turtle immer wieder an den Startpunk zurückkehren soll. Die Länge der Rückwärtsbewegung ist wie im ersten Fall
laenge/2, da wir genau die Strecke aus A. in E. zurückgehen.
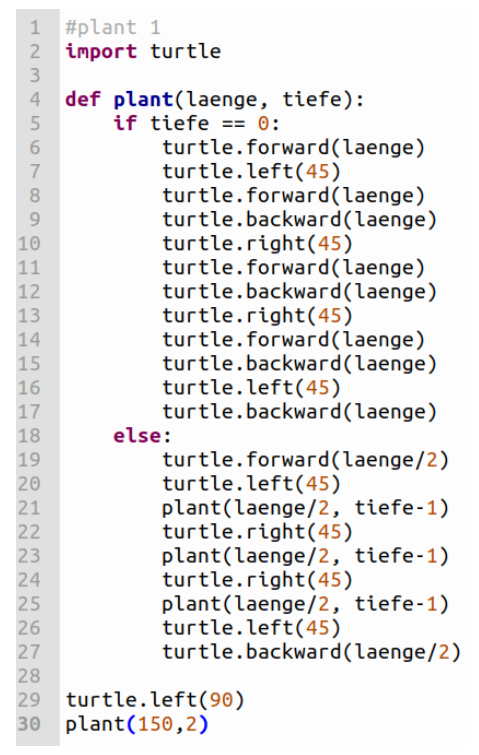
Rekursionsfall - L-System
Führe das Programm für verschiedene Rekursionstiefen aus. Färbe alle Zweige braun außer die Verzweigungen im Basisfall. Diese sollen grün sein. Benutze dafür den Befehl turtle.pencolor("green") und turtle.pencolor("brown").
Weitere L-Systeme zur Übung.
Dies kann man sich einfach ausdenken, indem man einen Spross zeichnt und dann bestimmt, welche Teile wie ersetzt werden sollen. Danach kann man dies rekursiv lösen.
Alternativ finden sich im Internet viele Ideen, indem man einfach nach Lindermayer-Systeme oder Fraktale sucht.