Ein Beispielautomat
Zum besseren Verständnis der formalen Definition und der Bestandteile eines endlichen Automaten betrachten wir nachfolgend einen Getränkeautomat.
Ein Cola-Automat
Das Sortiment unseres Automaten beschränkt sich auf Cola, die für 2€ erhältlich ist. Als klassischer Getränkeautomat akzeptieren wir nur Münzgeld. In diesem Fall kann der Nutzer 50ct, 1€ oder 2€ Münzen einwerfen. Die folgende Abbildung zeigt diesen Automaten.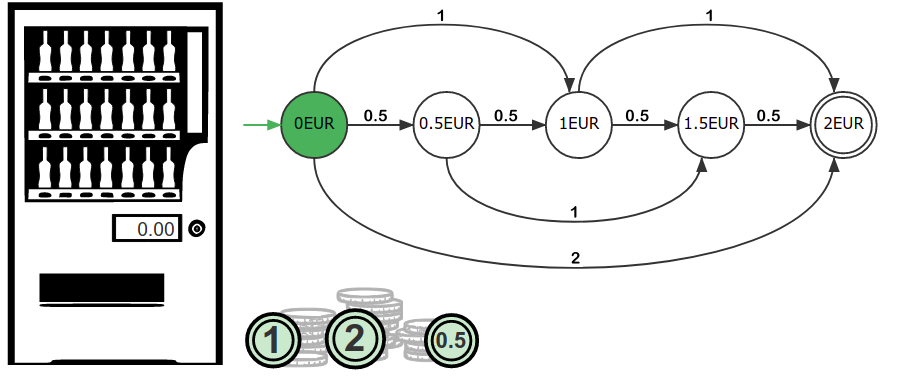
Aufgrund der möglichen Münzen, ergeben sich für den Automaten vier Zustände, die beim Münzeinwurf eingenommen werden können. Sobald der Nutzer Münzen im Wert von 2€ eingeworfen hat, gelangt er in einen akzeptierenden Zustand, dem Endzustand.
Formale Beschreibung
Für diesen Automaten ergibt sich folgende Zusammensetzung:
- \(Q = \{0\text{EUR}, 0.5\text{EUR}, 1\text{EUR}, 1.5\text{EUR}, 2\text{EUR}\}\)
- \(\sum = \{0.5, 1, 2\}\)
- \(q_0 = 0\text{EUR}\)
- \(\delta\) ist wie folgt definiert:
\(\hspace{0.1cm}\{\delta(0\text{EUR}, 0.5) = 0.5\text{EUR},\)
\(\hspace{0.3cm}\delta(0\text{EUR}, 1) = 1\text{EUR},\)
\(\hspace{0.3cm}\delta(0\text{EUR}, 2) = 2\text{EUR},\)
\(\hspace{0.3cm}\delta(0.5\text{EUR}, 0.5) = 1\text{EUR}, ...\}\) - \(F = \{2\text{EUR}\}\)
Wie funktioniert der Automat?
Beim Einwerfen der Münzen werden verschiedene Zwischenwerte erreicht, die wir als Zustände \(Q\) auffassen. Jeder Nutzer hat zu Beginn 0€ in den Automaten eingeworfen, weswegen dies den Startzustand \(q_0\) definiert. Von da aus gelangt man in die folgenden Zustände, indem man eine Münze einwirft, die \(\sum\) angehört.
Daraus ergeben sich auch die Übergänge \(\delta\), die definieren, von welchem Zwischenwert man mit welcher Münze einen neuen Zwischenwert erreicht. Entspricht der Zwischenwert dem Preis einer Cola von 2€, hat man den Endzustand der Endzustandsmenge \(F\) erreicht und das Kaltgetränk wird ausgeworfen.