Nichtdeterministische Endliche Automaten
Neben den DEA gibt es auch nichtdeterministische endliche Automaten (NEA). Im Gegensatz zu den DEA können NEAs mehrere Anfangszustände haben und für eine Eingabe unterschiedliche Ergebnisse zurückliefern. Bei einem NEA ist es also möglich, von einem Zustand mit dem gleichen Eingabesymbol mehrere Zustände zu erreichen.
Definition
Formal ähneln sich DEA und NEA sehr stark in ihrer Zusammensetzung: \(A = (Q, \sum, Q_0, \delta, F)\). Sie unterscheiden sich aber u.a. dahingehend, dass bei einem NEA mehrere Anfangszustände existieren können.
NEA sind wie folgt definiert:
- Die endliche Zustandsmenge \(Q\)
- Das endliche Eingabealphabet \(\sum\)
- Die Startzustandsmenge \(Q_0 \subseteq Q\)
- Die Übergangsfunktion \(\delta: Q \times \sum \rightarrow Q\)
- Die Endzustandsmenge \(F \subseteq Q\)
Ein weiterer Unterschied stellen die Übergänge dar, was am folgenden Beispiel deutlich werden soll.
Beispiel
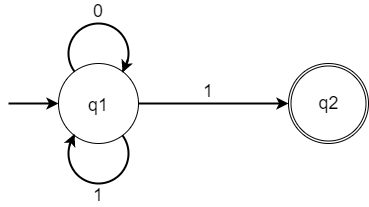
\(\delta(q1, 1) = {q_1, q_2}\)
Im Gegensatz zum DEA können bei einem NEA von einem Zustand mehrere Übergänge mit dem gleichen Eingabesymbol ausgehen. In diesem Fall erreichen wir vom Zustand \(q_1\) mit dem Eingabesymbol \(1\) sowohl den Zustand \(q_1\) als auch den Zustand \(q_2\), was dazu führt, dass für das gleiche Wort unterschiedliche Ergebnisse zurückgegeben werden können.
Ein Beispiel für ein solches Wort ist \(011\), welches der Automat sowohl akzeptieren als auch ablehnen kann:
| Zustandsfolge | Ergebnis |
|---|---|
| \(q_1 q_1 q_2 ?\) | Abgelehnt (fehlender Übergang) |
| \(q_1 q_1 q_1 q_2\) | Akzeptiert |